ESTADISTICAS 6 GRADO.

  PROFESOR: ING. DINA LUZ LEON SOLANO

TRANSCRIBIR AL CUADERNO EL CONCEPTO DE MEDIA ARITMETICA Y RESOLVER EL PUNTO 1 (MEDIA)  DE LA PAGINA 165

MEDIDAS DE TENDENCIA CENTRAL

El promedio de notas es muy importante.

Supóngase que un determinado alumno obtiene 35 puntos en una prueba de matemática. Este puntaje, por sí mismo tiene muy poco significado a menos que podamos conocer el total de puntos que obtiene una persona promedio al participar en esa prueba, saber cuál es la calificación menor y mayor que se obtiene, y cuán variadas son esas calificaciones.
En otras palabras, para que una calificación tenga significado hay que contar con elementos de referencia generalmente relacionados con ciertos criterios estadísticos.
Las medidas de tendencia central (media, mediana y moda) sirven como puntos de referencia para interpretar las calificaciones que se obtienen en una prueba.
Volviendo a nuestro ejemplo, digamos que la calificación promedio en la prueba que hizo el alumno  fue de 20 puntos. Con este dato podemos decir que la calificación del alumno se ubica notablemente sobre el promedio. Pero si la calificación promedio fue de 65 puntos, entonces la conclusión sería muy diferente, debido a que se ubicaría muy por debajo del promedio de la clase.
En resumen, el propósito de las medidas de tendencia central es:
Mostrar en qué lugar se ubica la persona promedio o típica del grupo.
Sirve como un método para comparar o interpretar cualquier puntaje en relación con el puntaje central o típico.
Sirve como un método para comparar el puntaje obtenido por una misma persona en dos diferentes ocasiones.
Sirve como un método para comparar los resultados medios obtenidos por dos o más grupos.
Las medidas de tendencia central más comunes son:
La media aritmética: comúnmente conocida como media o promedio. Se representa por medio de una letra M o por una X con una línea en la parte superior.
La mediana: la cual es el puntaje que se ubica en el centro de una distribución. Se representa como Md.
La moda: que es el puntaje que se presenta con mayor frecuencia en una distribución. Se representa Mo.

La media, el mejor dato.

De estas tres medidas de tendencia central, la media es reconocida como la mejor y más útil. Sin embargo, cuando en una distribución se presentan casos cuyos puntajes son muy bajos o muy altos respecto al resto del grupo, es recomendable utilizar la mediana o la moda. (Porque dadas las características de la media, esta es afectada por los valores extremos).
La media es considerada como la mejor medida de tendencia central, por las siguientes razones:
Los puntajes contribuyen de manera proporcional al hacer el cómputo de la media.
Es la medida de tendencia central más conocida y utilizada.  
Las medias de dos o más distribuciones pueden ser fácilmente promediadas mientras que las medianas y las modas de las distribuciones no se promedian.
La media se utiliza en procesos y técnicas estadísticas más complejas mientras que la mediana y la moda en muy pocos casos.

COMO CALCULAR LA MEDIA:

Media aritmética 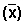o promedio

Es aquella medida que se obtiene al dividir la suma de todos los valores de una variable por la frecuencia total. En palabras más simples, corresponde a la suma de un conjunto de datos dividida por el número total de dichos datos.

Ejemplo 1:
En matemáticas, un alumno tiene las siguientes notas:  4, 7, 7, 2, 5, 3
n = 6 (número total de datos)

La media aritmética de las notas de esa asignatura es 4,8. Este número representa el promedio.
Ejemplo 2:
Cuando se tienen muchos datos es más conveniente agruparlos en una tabla de frecuencias y luego calcular la media aritmética. El siguiente cuadro con las medidas de 63 varas de pino lo ilustra.

Largo (en m)	Frecuencia absoluta	Largo por Frecuencia absoluta
5	10	5          .       10  =   50
6	15	6          .        15 =   90
7	20	7          .        20 =  140
8	12	8          .        12 =    96
9	6	9            .          6 = 54
	Frecuencia total = 63	430

Se debe recordar que la frecuencia absoluta indica cuántas veces se repite cada valor, por lo tanto, la tabla es una manera más corta de anotar los datos (si la frecuencia absoluta es 10, significa que el valor a que corresponde se repite 10 veces).